试题题目：
【简述题】
2009-2013年国内某航空公司使用B737-800飞机的日利用率分别为8.4、8.5、8.3、8.6和8.4轮挡飞行小时。利用简单算术平均法预测2014年该公司B737-800飞机的日利用率。
试题解析：
首先，判断时间序列各数值的位置关系。利用散点图判断。
散点图表示因变量随自变量而变化的大致趋势，据此可以选择合适的函数对数据点进行拟合。而所谓拟合是指已知某函数的若干离散函数值{f1，f2，…，fn}，通过调整该函数中若干待定系数f（λ1，λ2，…，λn），使得该函数与已知点集的差别（最小二乘意义）最小。如果待定函数是线性，就叫线性拟合或者线性回归（主要在统计中），否则叫作非线性拟合或者非线性回归。
例题中时间序列各数值散点图见考试指导用书第32页图3-1。由图可知，各期数值围绕其简单算术平均数对应的水平线上下波动，因而，得出结论，此题可以采取简单算术平均法预测。
因而，2014年该公司B737-800飞机的日利用率
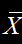=（8.4+8.5+8.3+8.6+8.4）/5=8.44。
8.44轮挡飞行小时是点估计值，需要运用置信区间进行可信程度判定。
置信区间给出的是被测量参数的测量值的可信程度，这个概率被称为置信水平。
可信度或者置信度常取95%或99%（95%置信区间的含义是估计值有95%的概率落在可信任范围内），实际工作中95%可信度更为常用。
试题答案：
详见解析