试题题目:
【单选题】
曼德制造公司利用下列模型确定金属M和金属片S的产品组合。
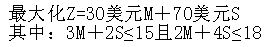
当M=2,S=3时的点:
A、位于顶点(拐角)上
B、是一个可行点
C、是最优的结果点
D、是一个不可行点
试题解析:
该问题涉及到线性规划的使用。线性规划是管理者基于约束条件做出使利润最大化或成本最小化决策时使用的解决问题的方法。它也可以用于解决许多其他的问题,比如资源最优配置。
线性规划的第一步是建立目标函数和约束条件。
在本题中,Z的最大值=30美元M+70美元S是目标函数。曼德制造公司生产M和S,并用利线性规划的方法确定最佳的产品组合。
本题的约束条件为:
3M+2S≤15
2M+4S≤18
非负约束:M,S≥0
利用代数方法解决该问题,并辅助以图形。
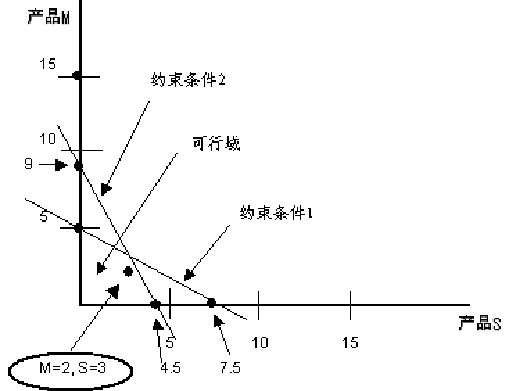
先计算X,Y在两端点的值,首先假设X为0,然后假设Y为0.
约束条件1:
3M+2S≤15
3×0+2×S≤15
2S≤15
S≤7.5
因此,第一个约束条件的图线与产品S轴交于7.5个单位处。
3M+2S≤15
3×M+2×0≤15
3M≤15
M≤5
因此,第一个约束条件的图线与产品M轴交于5个单位处。
约束条件2:
2M+4S≤18
2×0+4×S≤18
4S≤18
S≤4.5
因此,第二个约束条件的图线与产品S轴交于4.5个单位处。
2M+4S≤18
2×M+4×0≤18
2M≤18
M≤9
因此,第二个约束条件的图线与产品M轴交于9个单位处。
最优解在顶点处或两条约束直线的交点处。然而,在“可行域”任何一点都是可行的,尽管它不是最优的。点M=2,S=3位于可行域范围内,所以它被认为是一个可行点。
试题答案:
详见解析